迭代重建算法的基本思想
基本思想
图像重建除了通过中心切片定理来实现外,还可以通过解线性方程组来得到。对于二维图像就是像素,对于三维图像就是体素。
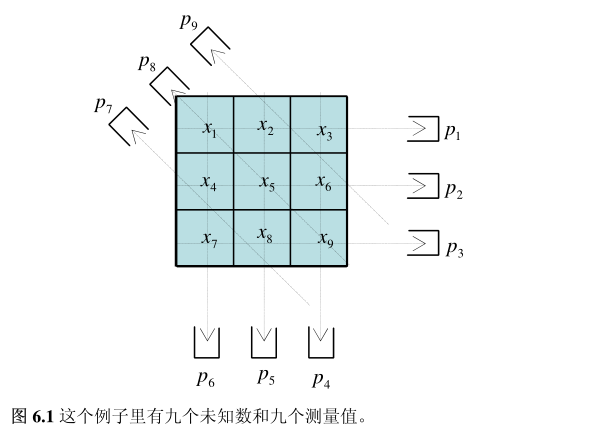
$\left{\begin{array}{c}x_{1}+x_{2}+x_{3}=p_{1} \ x_{4}+x_{5}+x_{6}=p_{2} \ x_{7}+x_{8}+x_{9}=p_{3} \ x_{3}+x_{6}+x_{9}=p_{4} \ x_{2}+x_{5}+x_{8}=p_{5} \ x_{1}+x_{4}+x_{7}=p_{6} \ 2(\sqrt{2}-1) x_{4}+(2-\sqrt{2}) x_{7}+2(\sqrt{2}-1) x_{8}=p_{7} \ \sqrt{2} x_{1}+\sqrt{2} x_{5}+\sqrt{2} x_{9}=p_{8} \ 2(\sqrt{2}-1) x_{2}+(2-\sqrt{2}) x_{3}+2(\sqrt{2}-1) x_{6}=p_{9}\end{array}\right.$
这个方程组也可以用矩阵的形式写出
$$
AX=p
$$
其中,$X=\left[x_{1}, x_{2}, \ldots, x_{9}\right]^{T}, \quad P=\left[p_{1}, p_{2}, \ldots, p_{9}\right]^{T}$迭代算法的思想使将$AX=p$变换成,迭代形式
$$
X^{(i+1)}=GX^{(i)}+b
$$
通过不同的变换方式变成迭代格式,就长生了不同的的迭代算法。比如:
常用迭代算法
代数迭代重建技术(ARO,algebraic reconstruction technique)
ART 算法是个“行运算”算法。它每次考虑一条射线就更新一次图像。ART 算法的表达式是
$$
X^{下一个}=X^{\text {当前}}-\frac{A_{i} X^{\text {当前}}-p_{i}}{\left|A_{i}\right|^{2}} A_{i}^{T}
$$
$A_iX$ 执行的是沿着第$i$条射线的投影运算,$p_i$ 是在第 $i $个探测像元上测到的投影数据,$\left|A_{i}\right|^{2}=\sum_{j} a_{i j}^{2}$是沿着第 $i$ 条射线上各“贡献”因子的平方和,$cA^{T}{i}$ 是把数值 $c $沿着第$ i$ 条射线做反投影。如果我们把上面的算法改写成下面的形式 .
$$
X^{\text {next }}=X^{\text {current }}-\left(\frac{A{i} X^{\text {current }}}{\left|A_{i}\right|}-\frac{p_{i}}{\left|A_{i}\right|}\right) \frac{A_{i}^{T}}{\left|A_{i}\right|}
$$
该算法的几何意义就比较明显了:
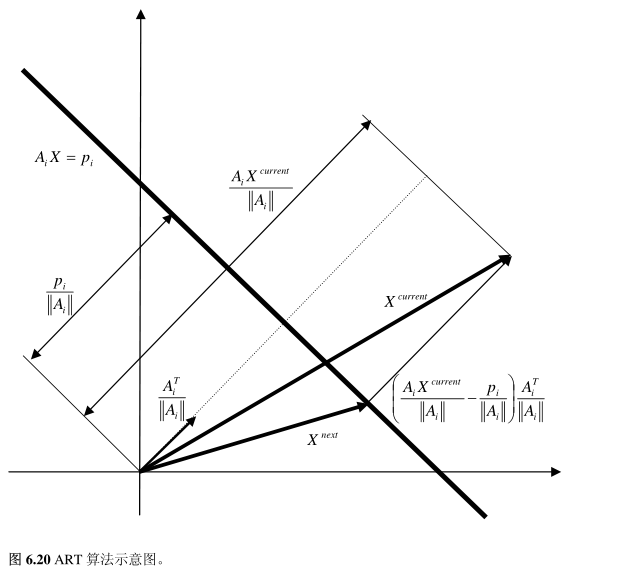
最大期望极大似然算法(ML-EM,Maximum-Likelihood Expectation-Maximization)







参考文献:
[1] 曾更生,医学图像重建
