二维图像重建的一般流程
[toc]
❓什么是图像重建?
断层成像顾名思义就是要得到一个物体内部的截面图像。比如你想知道西瓜里面是什么样的,最简单的办法就是把西瓜切开 (图1.1)。显然对病人来说,这是万不可行之举。我们真想有个办法,不用动刀,就可把病人内部看得清清楚楚。
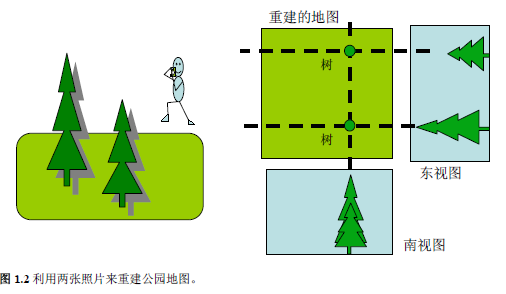
另一个例子。你想到一个美丽的街心公园去参观。可惜,公园正在维修,游人不得入内。你只好在公园的外围走走,拍几张照片。公园
内有两棵参天大树,极为壮观。你在公园的东面和南面对公园拍了照 ,颇为满意。回到家后,你用你的得意照片,居然画出了公园地图,并确定了那两棵树的位置 (图1.2右)。其实,要确定那两棵树的位置并不难。你只要把那两张照片按原本的方位放好。从照片上的每棵树画出一条垂线。

💫图像重建的算法思想是什么?
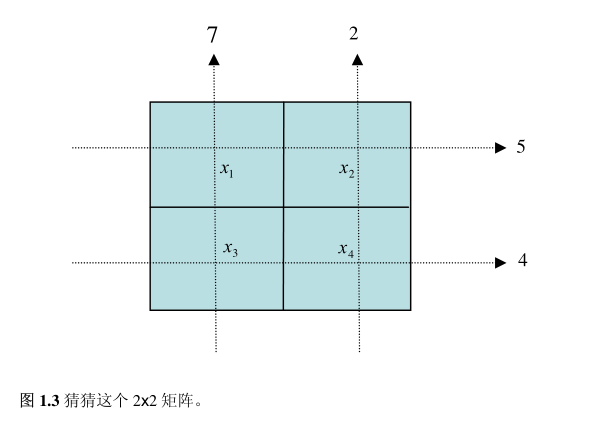
断层成像是个数学问题。让我们一起做个有趣的数学习题吧。这里有个 2x2 的矩阵。 矩阵中的元素的数值暂时保密。我给你一些暗示: 第一行的和是 5。第二行的和是 4。第一列的和是 7。第二列的和是 2 (图1.3)。你可以算出这个 2x2 矩阵吗?
这个问题可以用解方程组的方法解决。设那些矩阵元素为未知数,列一个线性方程组:
$$
\begin{equation}
\begin{aligned}
x_1+x_2=5;\
x_3+x_4=4;\
x_1+x_3=7;\
x_2+x_4=2;\
\end{aligned}
\end{equation}
$$
解这个方程组便得到;
$$
\begin{equation}x_1=3,x_2=2,x_3=4,x_4=0\end{equation}
$$
通过探测物体的投影数据,重建出物体的实际内部构造。这就是图像重建的一般思想。
✔图像重建算法的数学基础有哪些?
🍕中心切片定理
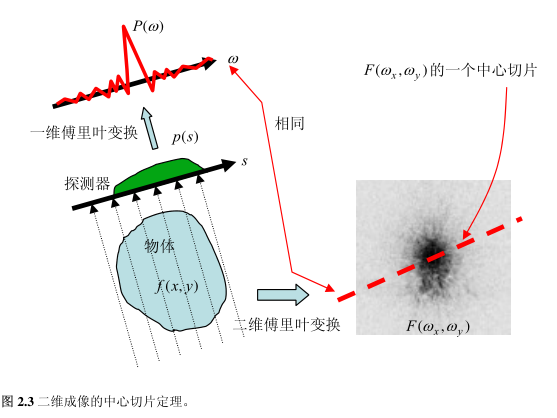
中心切片定理是断层成像的理论基础。这个定理还有其它的称谓,如投影切片定理和傅里叶中心切片定理。二维图像的中心切片定理指出:二维函数 f(x, y) 的投影 p(s) 之傅里叶变换 P(ω) 等于函数 f(x, y) 的傅里叶变换 F(ωx, ωy) 沿与探测器平行的方向过原点的片段。
🚩为什么要引入滤波?

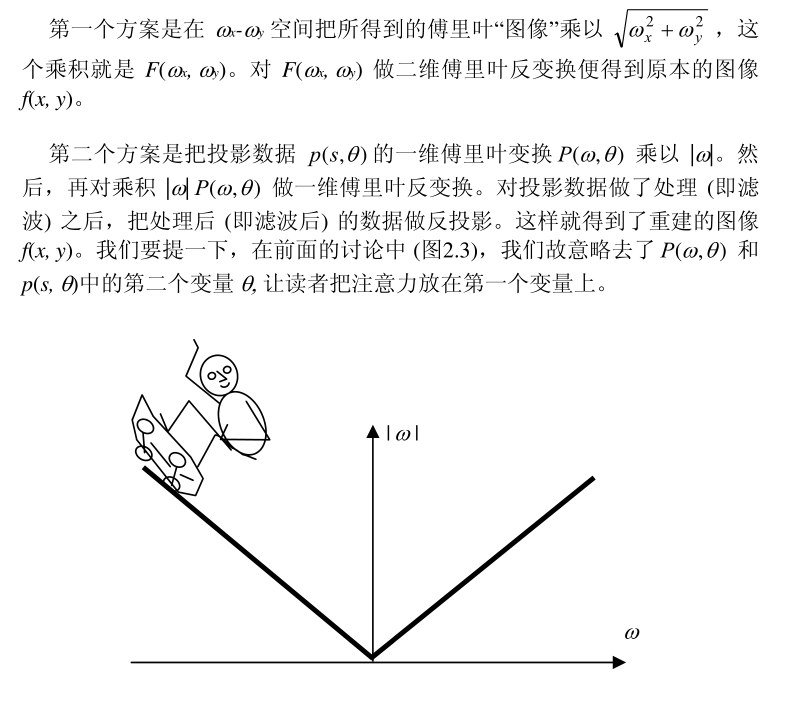
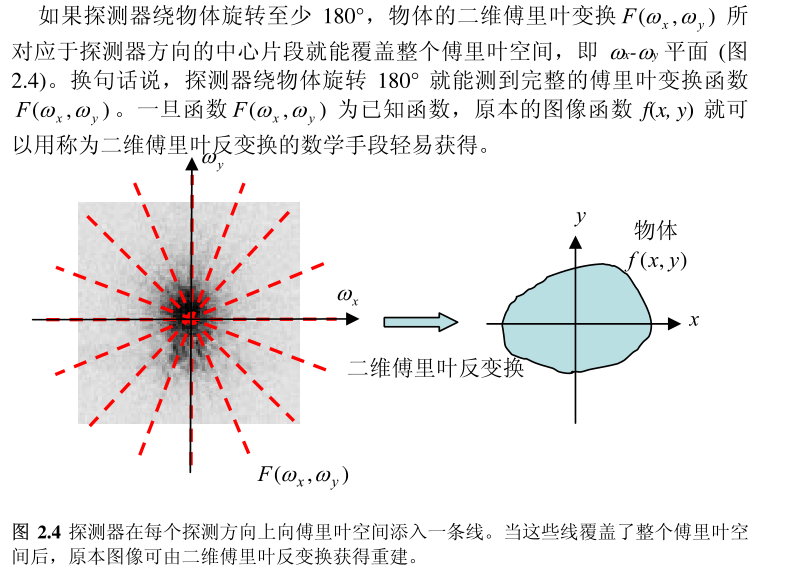
第二个方案通常被称作处理FBP (Filtered Backprojection 先滤波后反投影) 算法。第二个方案比第一个方案知名度高得多。在断层成像领域里,函数|ω| 被称作斜坡滤波器。
❤有哪些滤波重建方法?
==滤波的思想==:在中心切片定理中,旋转中心被切片涂抹的更浓密,这将导致图像像素比较均匀(低频区域;高频区域是指图像对比度比较大的图像边缘区域),进而重构的图像中心区域比较模糊。那么滤波器的思想是将中心切片函数乘以一个与旋转中心距离相关的权重因子,使得切片在图像上涂抹的比较均匀。这样重构出来的图像才不会出现旋转中心模糊的现象。下面介绍一下有哪些图像重建及滤波方法。
🛴方法1

🛵方法2

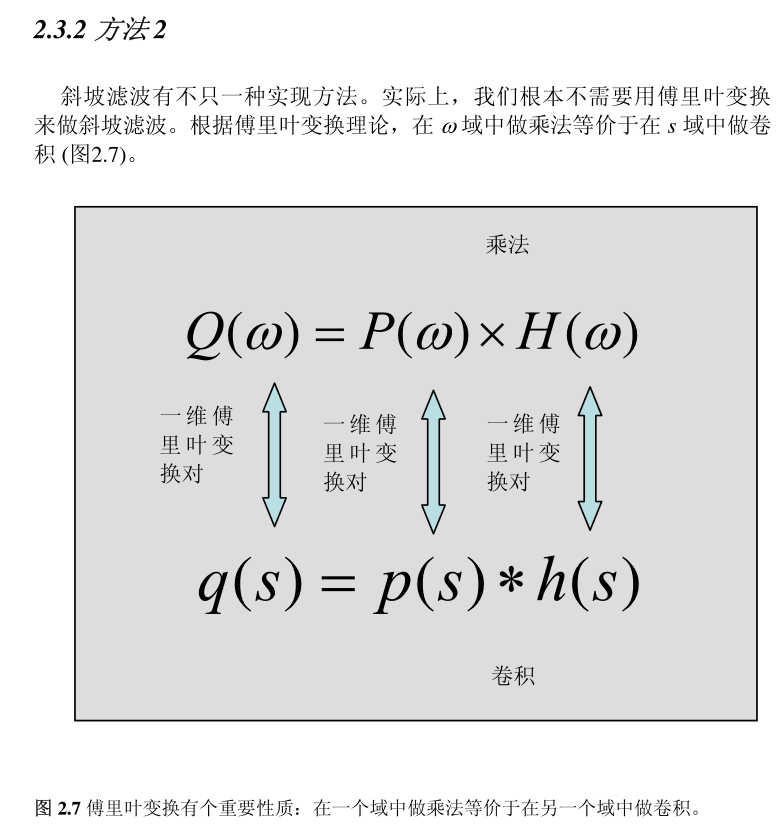
🏍方法3


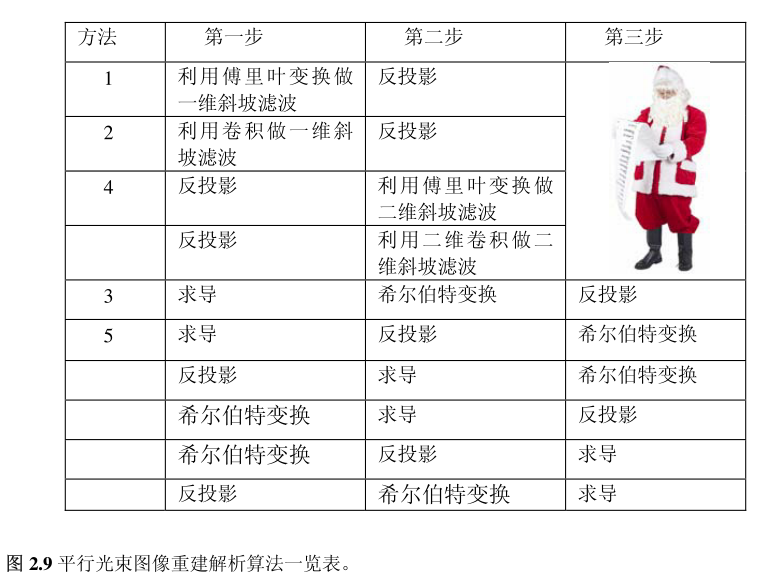
🧭算法一览表
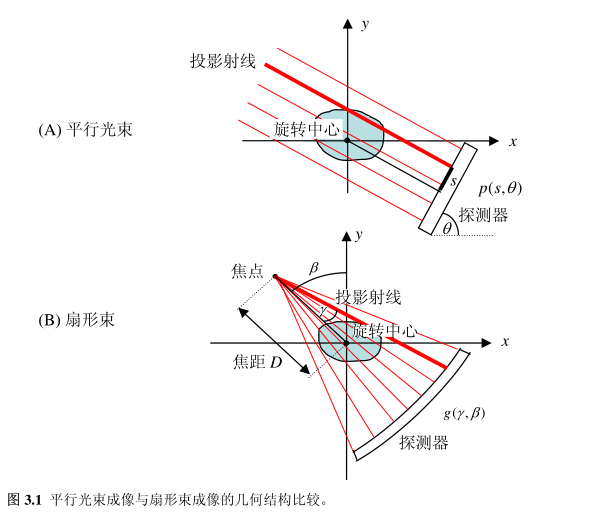
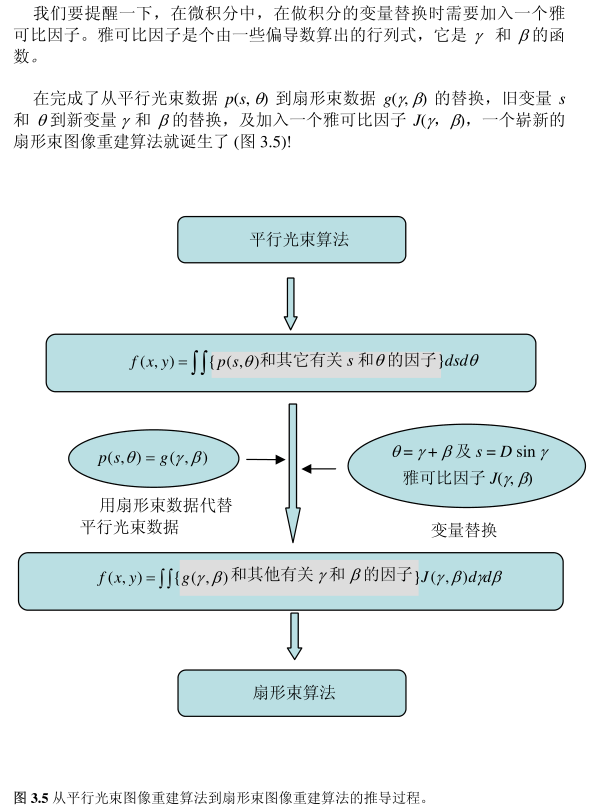
👼扇形束投影算法如何转换到平行束投影算法
==基本思想==:根据利用点扩散函数的移动不变性,可将扇形束投影重组成平行束投影;然而,在进行重组时将需要进行插值运算,这将导入不必要的误差。故而需要根据重组变换原理,采用变量替换原理,将适用于平行束投影算法中的变量替换成扇形束中的转换关系。
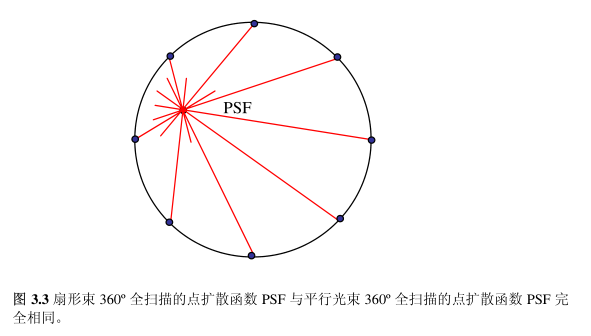
🍚点扩散函数的移动不变性
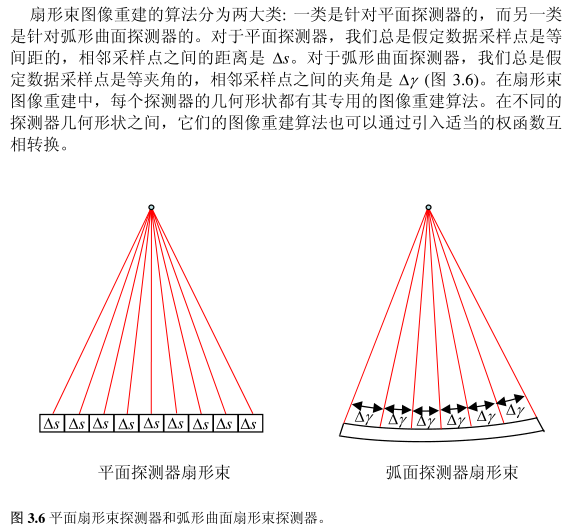
对于平行光束成像,我们用极为重要的中心切片定理推导出了一些图像重建的算法。可是,对与扇形束成像,我们并没有相应的中心切片定理。我们只好想个别的办法来推导扇形束的图像重建算法。这个办法就是把扇形束的成像问题转化成平行光束的成像问题,把平行光束图像重建的算法修正一下然后应用于解决扇形束的成像问题中。
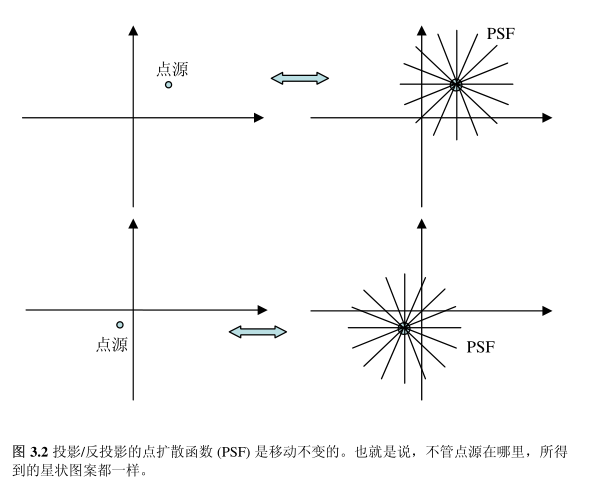
假定探测器是匀速地绕物体转动,而且数据采样的角度区间也是均匀的。在这个假设下,平行光束的投影/反投影的点扩散函数 (PSF) 是移动不变的。换句话说,如果你把一个点源放在 x-y 平面上。放到哪里到无所谓,只要放在探测器的视野内就好。
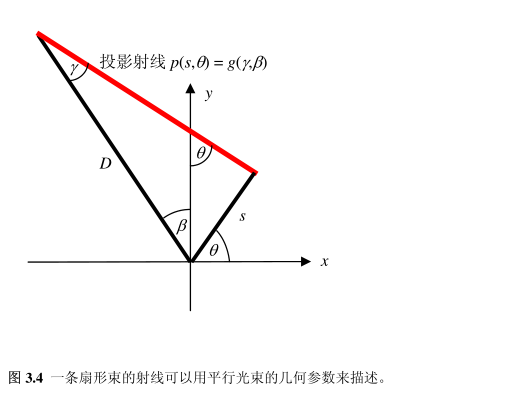
🍳扇形束射线如何用平行束来描述
一个直截了当的方法是把所有的扇形束射线放在一起进行分组,把互相平行的射线分在一组,这样就把扇形束的成像问题简化为平行光束的成像问题。正如图3.4所示,每一条扇形束的射线都刚好对应一条平行光束的射线。这两条线是完全重合的。也就是说,每一个扇形束的数据 g(γ, β) 都刚好对应一个平行光束的数据 p(s, θ),它们的坐标满足下列关系:
$$
\theta = \gamma +\beta \
s=Dsin\gamma
$$
其中 $$D$$ 为焦距,也就是从扇形的焦点到旋转中心的距离。当上面这两个关系成立时,这两个成像系统所测的数据是相同的:
$$
p(s,\theta)=g(\gamma,\beta)
$$

参考文献:
[1] 曾更生,医学图像重建
